レイアウトとは④ー「アイポイント」ー
こんばんは!プラオプ ハセガワです!
さてさて、「レイアウト作業」についてのお話。
前回は「頂点間距離」というものを解説いたしました。
今日はいよいよ「レイアウト」というものを考えてその結果、何が求められるのか?という内容です。
眼鏡の掛け具合を最適に合わせてもレイアウトをしなければ眼鏡の性能は正しく発揮されません。
レイアウトをしなかったら・・・
常にかけっぱなしの眼鏡「常用眼鏡」の場合、傾斜角度は5°〜10°
そして頂点間距離は12mmが適切
ではそれに当てはめて「傾斜角:10°」「頂点間距離:12mm」に眼鏡をフィッティングして合わせましょう。
で、レンズの中心はどこにするのか?
仮に真っ直ぐ前を向いたところにレンズの中心を合わせたとします。
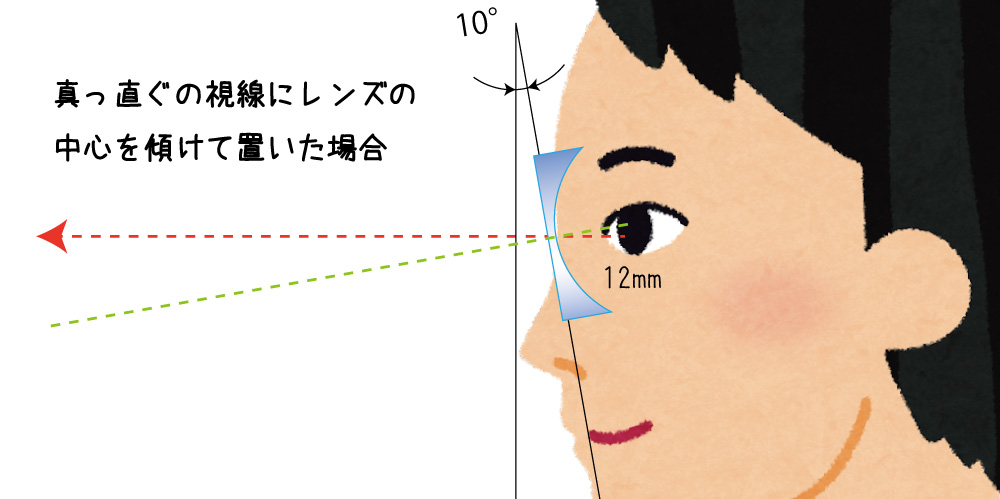
これだと前の前の記事でレンズメーターにレンズを傾けて測ると変な乱視が発生したように、レンズの中心を斜めに見る事になり度数がズレてしまう事になります。

「だから傾斜をつけるって言ったじゃん」
ですよねー
でもこれで問題になるのは「どこを見ても正確にならない」という事なのです。
ではレンズに直角に視線が通るように10°下を見る事にしましょう。そうすればレンズズレは無くなるはずです。
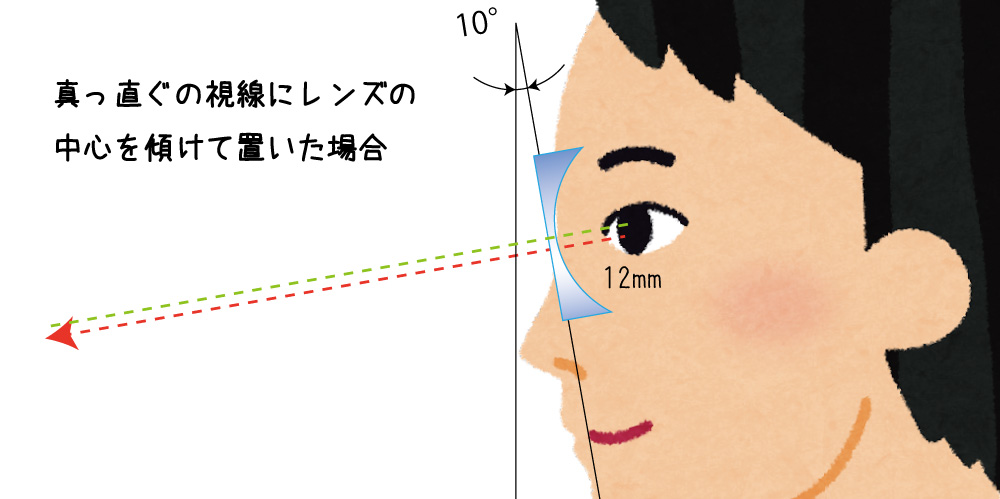
はい、視線はレンズに直角ですが、中心を通っていません。
そりゃそうです。中心は前を向いた時の高さのままなのですから。
頂点間距離が大きければその誤差はなおさら大きくなります。
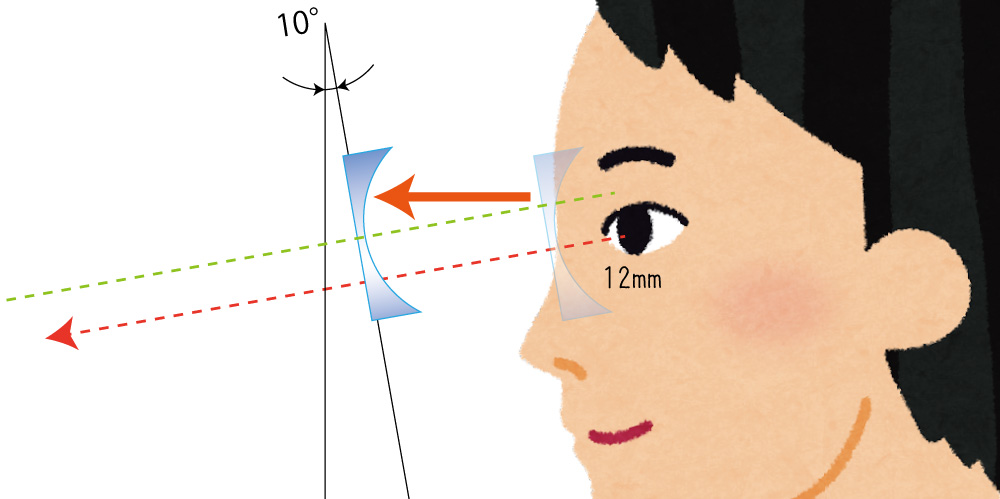
実はレンズの誤差は傾きだけではなく、中心ではない部分を真っ直ぐ見ても起きるのです。
それが下の写真
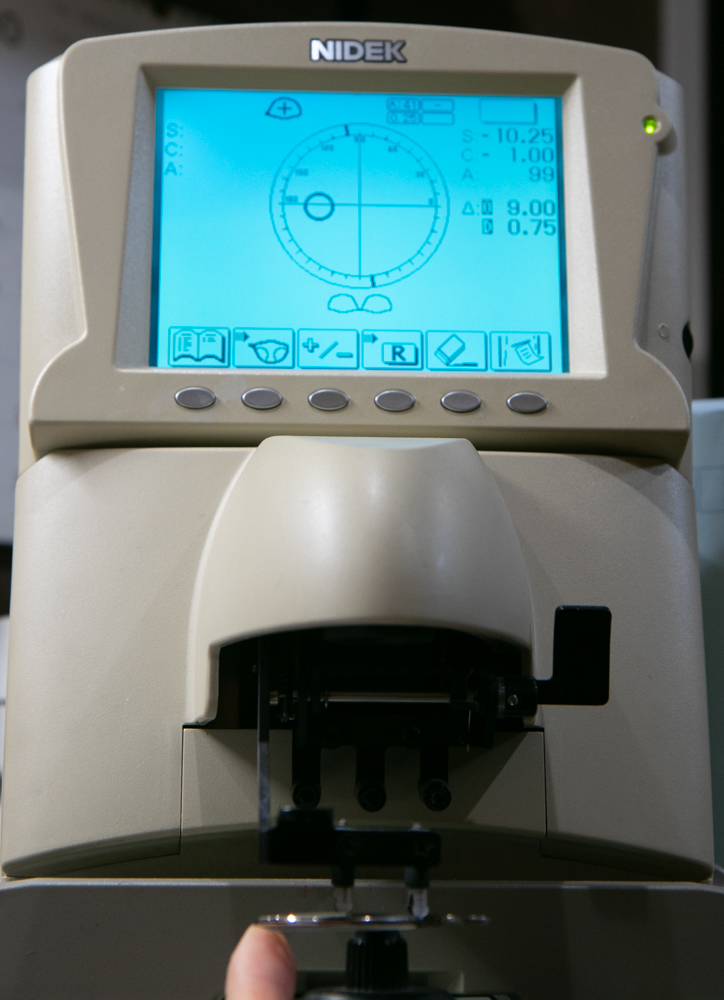
また「-10.00」を傾けるのはなく、水平にずらして中心から外れたところで測っています。すると「S-10.25 C-1.00 AX99」
つまり度数が強くなり、無いはずの乱視が発生していることを表しています。
レンズの傾斜と同じだけ視線を傾けても、視線がレンズの中心でないところを直角に通過しているのなら、これは極端に言えばどんな角度で見ても正確な度数が目に作用しないと言えてしまうわけです。
でもそれを最小限に抑える方法があります。その方法こそが「レイアウト作業」なのです。
傾斜角度と頂点間距離によってレイアウトが決まる
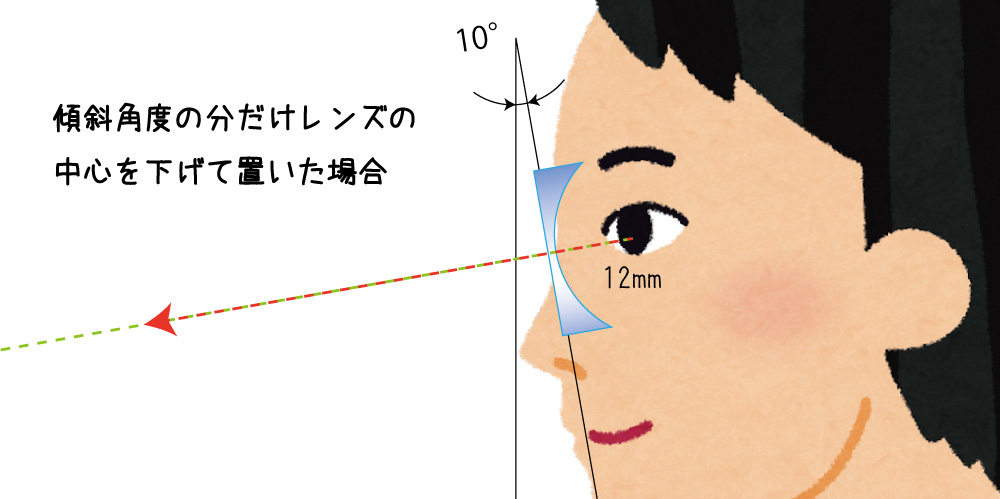
つまり、傾斜角度と同じだけ視線を下げたそのときに、レンズの中心を直角に視線が貫くようにすれば良いのです。
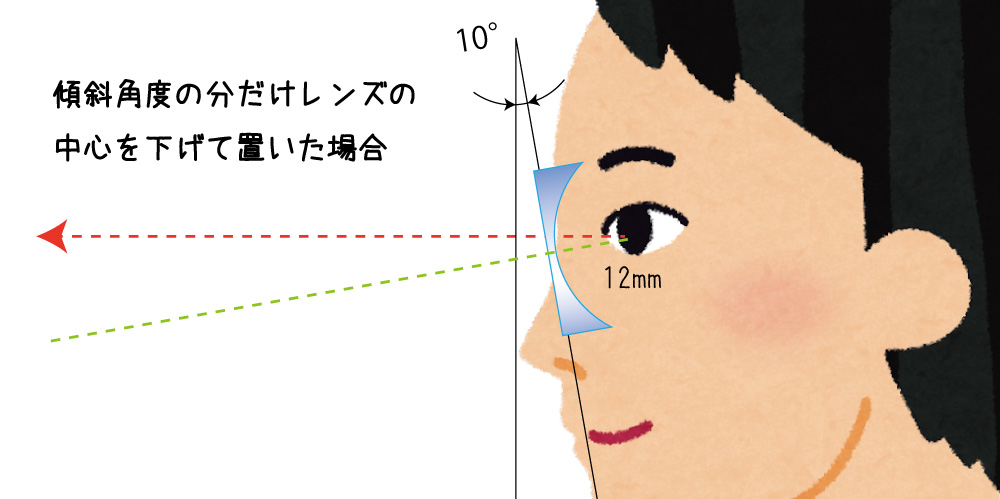
上のイラストでは、レンズの中心が若干下に来るように配置されています。
前のイラストと比較すると、真っ直ぐ前を向いた視線がレンズの中心ではない部分を貫いていることがわかります。
これが10°視線を下に向けたらどうるか?

レンズの中心と視線が直角に交差している事がわかります。
これが最も誤差を小さくできるレンズの配置です。
実はレンズは、中心以外の部分に視線が通るときにその位置に応じた斜めの角度で見た時に誤差が出ないように設計されているのです。
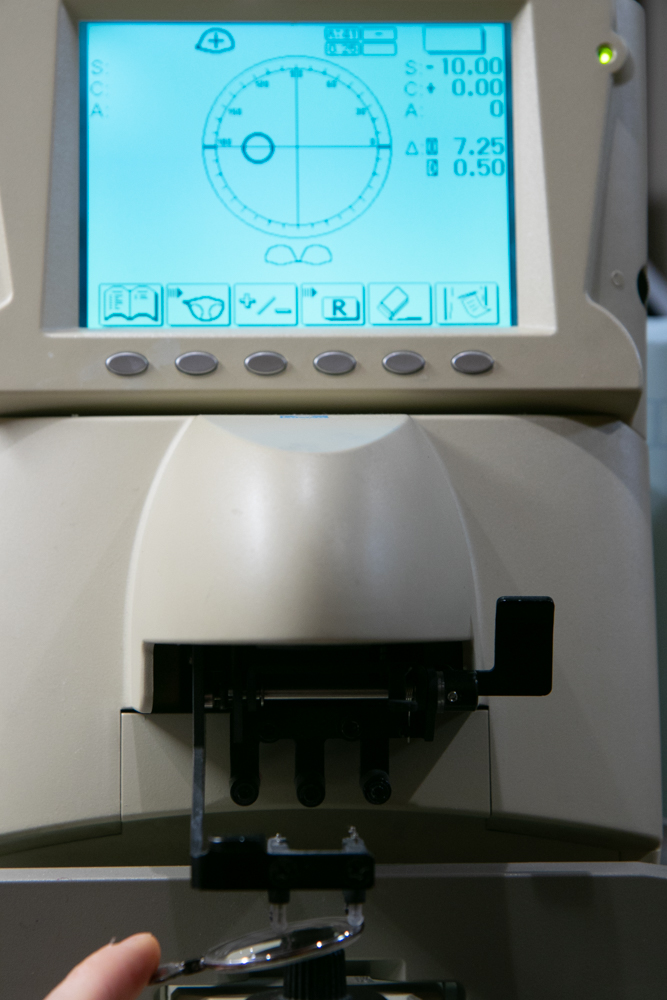
これは今までと違って「中心じゃない部分」を「斜めに」測定した状態です。
「-10.00」のレンズが綺麗に「-10.00」と表示されております。
(といっても限界はあるので、あまり斜めに視線は通したくありません。だから傾斜角度をつけるのです)
こうなるようにレンズの形の湾曲具合は考えられており、さらには「非球面設計」の主な目的は、この「周辺部分を斜めに見たときでも誤差が起きない」ことを目標にしているわけです。決して「レンズを薄くする」事が主目的ではありません。
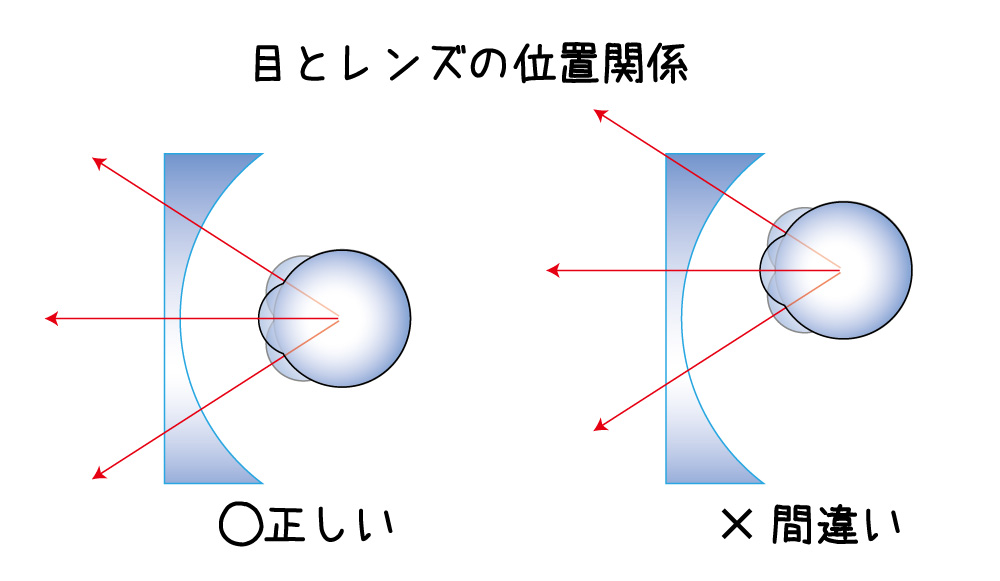
頂点間距離が大きくなれば、レンズはより一層下げなければなりません。
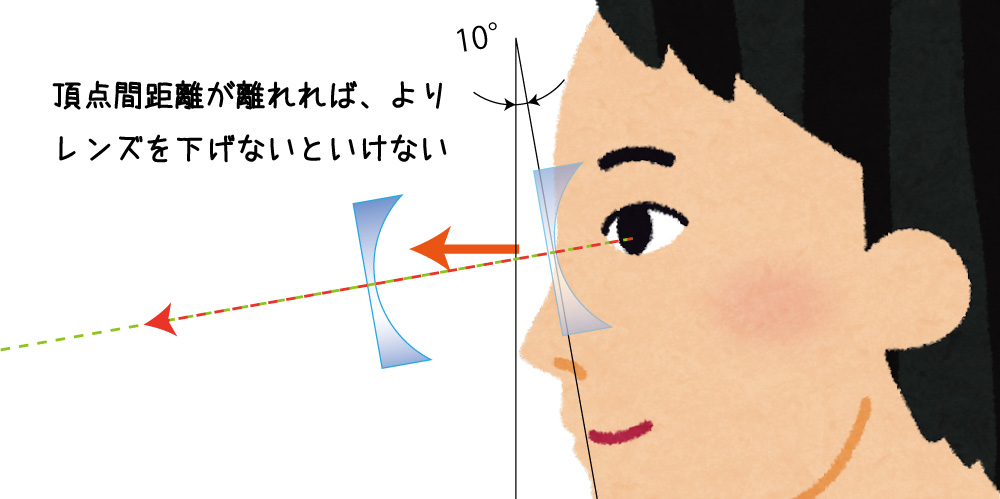
結論は「傾斜角度が付いたレンズの中心を、視線が直角に貫くような位置を出す」
これが「レイアウト作業」というわけです。
適切にレイアウトを行えば、レンズの中心の位置は真っ直ぐ前を向いた視線の位置よりも傾斜角度と頂点間距離の分だけ下に下がる事になります。
この位置こそが「アイポイント(EP:Eye Point)」と呼ばれるレンズの高さの数値になるわけです。
ただしこれは、いわゆる普通の眼鏡レンズのお話。
遠近両用などはもっと深いですし、そもそも理想の状態からのズレをレンズ側で補ってしまう高性能なレンズも出ております。
そういうレンズは昔は滅茶苦茶高価でしたが今は割とお求めやすくなり出ております。(といっても五千円じゃあ買えませんが・・・)
さて「アイポイント」をどう考えたらいいのかは分かりました。
しかし「レイアウト作業」を行うには具体的に、「傾斜角度」「頂点間距離」そして後ほど出てくる「反り角度」という眼鏡の掛かり具合を測定しなければなりません。
次回はそのへんのお話です。


この記事へのコメントはありません。